Comparison, profiling and optimizing with paralleling.
During the development of a game data viewing tool for a space simulator, I encountered a need to calculate all shortest paths between 2218 vertices, having 30250 edges in a directional graph. That is required to calculate profit per time, for different trading routes in a game of flying between star systems and trading. ^_^.
I started with a simple algorithm of a Floyd Warshal to calculate all paths. By taking a page from Wikipedia about it I implemented it in Golang and measured the results
floyd.go
package trades
import (
"fmt"
"math"
)
/*
floydWarshall algirthm
*/
type Floyder struct {
*GameGraph
dist [][]int
}
var FloydMax = int(math.MaxInt / 2)
func (f *Floyder) mapMatrixEdgeToFloyd(keya VertexName, keyb VertexName, distance int) {
f.dist[f.IndexByNick[keya]][f.IndexByNick[keyb]] = distance
}
func NewFloyder(graph *GameGraph) *Floyder {
f := &Floyder{GameGraph: graph}
return f
}
func (f *Floyder) Calculate() *Floyder {
len_vertexes := len(f.matrix)
f.dist = make([][]int, len_vertexes)
for i := 0; i < len_vertexes; i++ {
f.dist[i] = make([]int, len_vertexes)
for j := 0; j < len_vertexes; j++ {
f.dist[i][j] = FloydMax
}
}
for i := 0; i < len_vertexes; i++ {
f.dist[i][i] = 0
}
index := 0
for vertex, _ := range f.matrix {
f.IndexByNick[vertex] = index
index++
}
for vertex_source, vertex_targets := range f.matrix {
for vertex_target_name, vertex_target_dist := range vertex_targets {
f.mapMatrixEdgeToFloyd(vertex_source, vertex_target_name, int(vertex_target_dist))
}
}
for k := 0; k < len_vertexes; k++ {
if k%100 == 0 {
fmt.Println("starting, k=", k)
}
for i := 0; i < len_vertexes; i++ {
for j := 0; j < len_vertexes; j++ {
if f.dist[i][k]+f.dist[k][j] < f.dist[i][j] {
f.dist[i][j] = f.dist[i][k] + f.dist[k][j]
}
}
}
}
return f
}
floyd_test.go: Unit test for launch
package trades
import (
"fmt"
"math"
"testing"
)
func TestFloyd(t *testing.T) {
fmt.Println(math.MaxFloat32)
graph := NewGameGraph()
// floyd := NewFloyder()
graph.SetEdge("a", "b", 5)
graph.SetEdge("a", "d", 10)
graph.SetEdge("b", "c", 3)
graph.SetEdge("c", "d", 1)
floyd := NewFloyder(graph)
floyd.Calculate()
dist := floyd.dist
for i := 0; i < 4; i++ {
for j := 0; j < 4; j++ {
if dist[i][j] == FloydMax {
fmt.Printf("%7s", "INF")
} else {
fmt.Printf("%7d", dist[i][j])
}
}
fmt.Println()
}
fmt.Println("a -> c = ", GetDist(graph, dist, "a", "c"))
fmt.Println("a -> b = ", GetDist(graph, dist, "a", "b"))
fmt.Println("a -> b = ", GetDist(graph, dist, "a", "d"))
}
Unfortunately, the calculations it showed were too slow on the desired graph size mentioned before.
floyd:
floyder.GetDist("li01_01_base", "li01_to_li02")= 22154.047859719714
floyder.GetDist("li01_to_li02", "li02_to_li01")= 0
floyder.GetDist("li02_to_li01", "li12_02_base")= 9239.98628904769
GetDist(graph, dist, "li01_01_base", "li01_02_base") 21397.06209135834
GetDist(graph, dist, "li01_01_base", "br01_01_base") 128222.95301963031
GetDist(graph, dist, "li01_01_base", "li12_02_base") 31394.034148767405
time=2024-06-16T12:29:47.108+02:00 level=DEBUG msg="time_measure 2m20.534426392s | trade routes calculated"
Initially, it took more than 2 minutes and 20 seconds to calculate the necessary data with Floyd, which happened because of float64 usage. The time improved considerably to just 60 seconds if using integers instead of floats for a matrix though. The example above is already of a fixed-to-integer usage algorithm.
The speed was not very satisfying, therefore it made me look further. Can I parallel this algorithm to speed up? The found article from a university hints at yes. However the algorithm looked dependent on previous parallelized jobs, it looked too complex, so I did not risk implementing it. Trustworthy code examples are rather tough to find for parallel Floyd too.
Looking through my options on the shortest paths algorithm Wikipedia page, I saw that Johnson’s algorithm is very promising, as it is told to be possibly faster on sparse graph
I checked the geeks website for inspiration on how to implement it, as it already had implementations in C++, Java, Python and Javascript. By rewriting the Java algorithm to Golang, I received a speed almost equal to Floyd’s calculations with integers. (Initially, I thought it was twice faster since I discovered Integer optimization for Floyd later)
GetDist(graph, dist, "li01_01_base", "li01_to_li02")= 22148
GetDist(graph, dist, "li01_to_li02", "li02_to_li01")= 0
GetDist(graph, dist, "li02_to_li01", "li12_02_base")= 9235
GetDist(graph, dist, "li01_01_base", "li01_02_base") 21389
GetDist(graph, dist, "li01_01_base", "br01_01_base") 128172
GetDist(graph, dist, "li01_01_base", "li12_02_base") 31383
time=2024-06-16T12:33:57.060+02:00 level=DEBUG msg="time_measure 1m12.256099084s | trade routes calculated"
It was still a rather horrible time to calculate it. What did I do next? I turned on the default Golang profiling. By just adding extra code lines from std lib into the unit test beginning. Rrunning after that go tool pprof johnson.prof and then inserting command web. That opened the browser page with the visual profile shown below.
func TestTradeRoutesJohnson(t *testing.T) {
//The code i don't wish to profile
configs := configs_mapped.TestFixtureConfigs()
graph := MapConfigsToFloyder(configs, WithFighterPaths(false))
// for profiling only stuff.
f, err := os.Create("johnson.prof")
if err != nil {
log.Fatal(err)
}
pprof.StartCPUProfile(f)
defer pprof.StopCPUProfile()
// Code i wish to profile
timeit.NewTimerF(func(m *timeit.Timer) {
johnson := NewJohnsonFromGraph(graph)
var dist [][]int = johnson.Johnsons()
fmt.Println(`GetDist(graph, dist, "li01_01_base", "li01_to_li02")=`, GetDist(graph, dist, "li01_01_base", "li01_to_li02"))
fmt.Println(`GetDist(graph, dist, "li01_to_li02", "li02_to_li01")=`, GetDist(graph, dist, "li01_to_li02", "li02_to_li01"))
fmt.Println(`GetDist(graph, dist, "li02_to_li01", "li12_02_base")=`, GetDist(graph, dist, "li02_to_li01", "li12_02_base"))
dist1 := GetDist(graph, dist, "li01_01_base", "li01_02_base")
dist2 := GetDist(graph, dist, "li01_01_base", "br01_01_base")
dist3 := GetDist(graph, dist, "li01_01_base", "li12_02_base")
fmt.Println(`GetDist(graph, dist, "li01_01_base", "li01_02_base")`, dist1)
fmt.Println(`GetDist(graph, dist, "li01_01_base", "br01_01_base")`, dist2)
fmt.Println(`GetDist(graph, dist, "li01_01_base", "li12_02_base")`, dist3)
assert.Greater(t, dist1, 0)
assert.Greater(t, dist2, 0)
assert.Greater(t, dist3, 0)
}, timeit.WithMsg("trade routes calculated"))
}
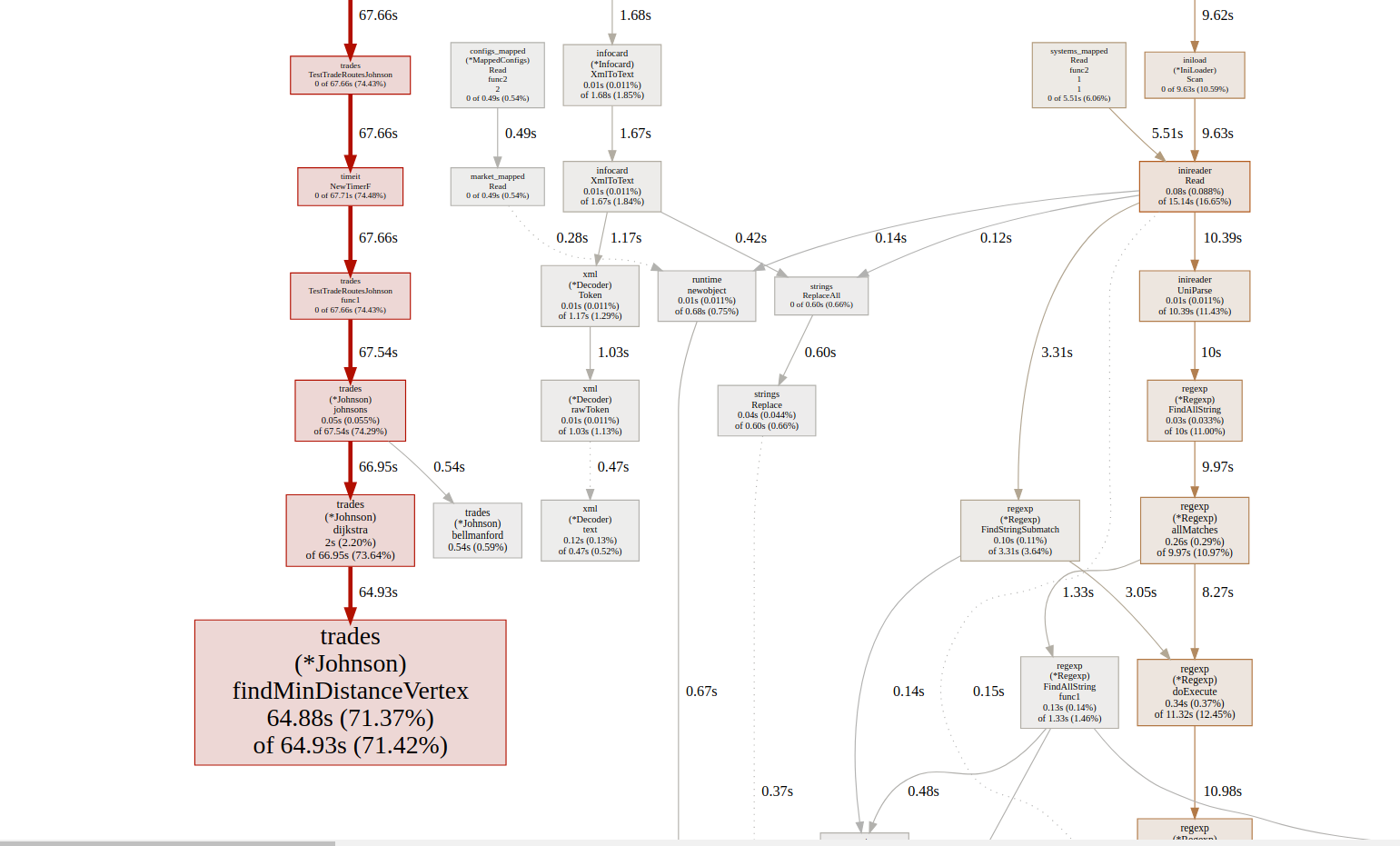
I discovered that the provided Java algorithm had a problem with its findMinDistanceVertex function. After comparing the Java algorithm with C++ and Python algorithms (on the same page) I saw they use Priority Queue data structure, while Java just used search in a list. Suspecting not efficiency from it, I rewrote Dijkstra’s algorithm to usage of Priority Queue, by taking info for it from this Golang std library for heap ( Later was discovered that the Wiki page for Dijkstra ( https://en.wikipedia.org/wiki/Dijkstra’s_algorithm ) actually documents both those versions and tells their complexity, the heap version is obviously better )
GetDist(graph, dist, "li01_01_base", "li01_to_li02")= 22148
GetDist(graph, dist, "li01_to_li02", "li02_to_li01")= 0
GetDist(graph, dist, "li02_to_li01", "li12_02_base")= 9235
GetDist(graph, dist, "li01_01_base", "li01_02_base") 21389
GetDist(graph, dist, "li01_01_base", "br01_01_base") 128172
GetDist(graph, dist, "li01_01_base", "li12_02_base") 31383
time=2024-06-16T14:02:39.834+02:00 level=DEBUG msg="time_measure 28.153478383s | trade routes calculated"
The results were promising. Now the algorithm was calculated in just 28 seconds! But I wished faster, as it was still not enough for me. I wondered how to improve it
Running the profiler again I saw all the slowness coming from calculating Dijkstra’s algorithms as part of Johnson’s algorithm
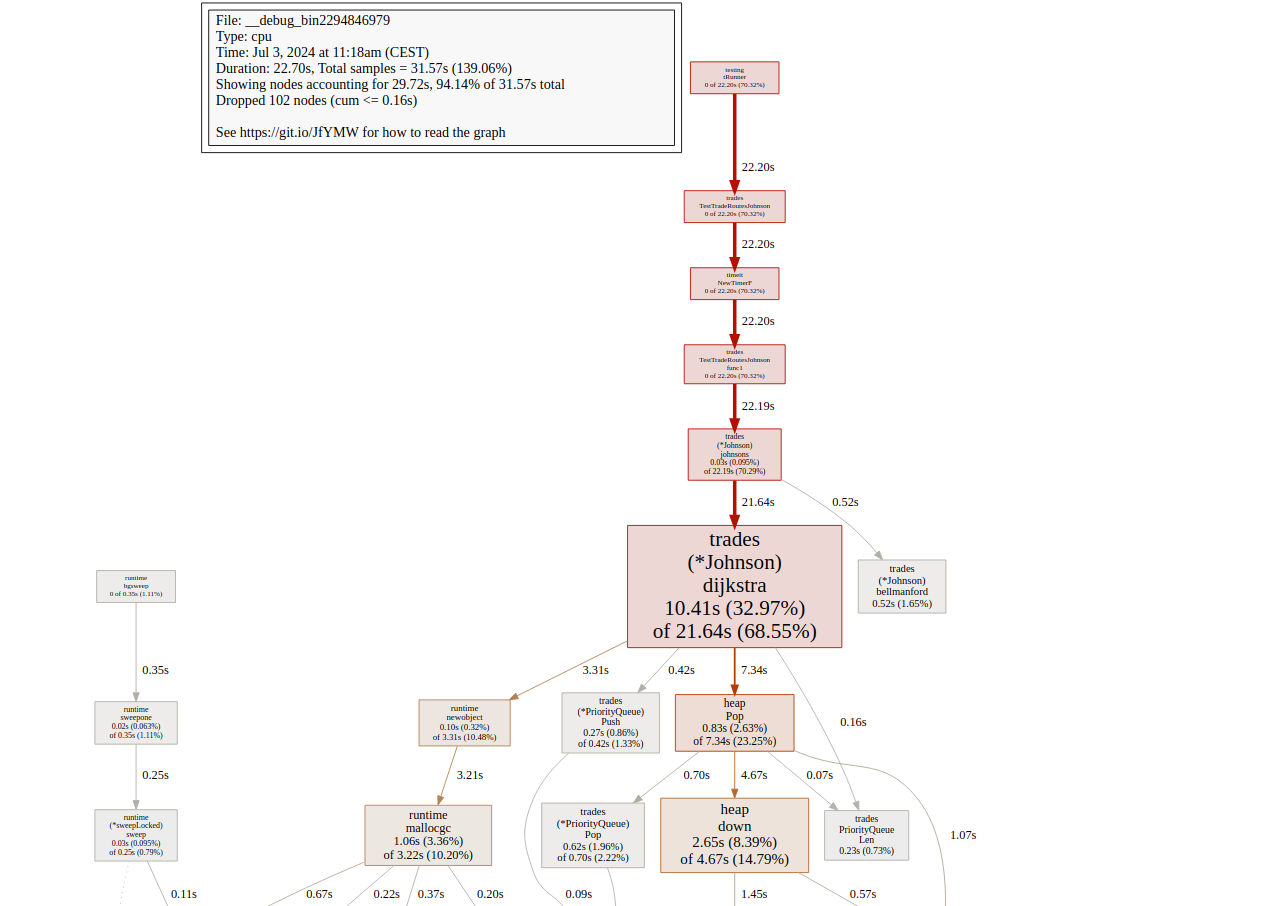
Checking the code I noticed rather an easy spot for parallelization, as calculations looked independent and used the same read-only data.
func (g *Johnson) johnsons() [][]int {
// ...Other Johnson Code
var distances [][]int = make([][]int, g.vertices)
for s := 0; s < g.vertices; s++ {
distances[s] = g.dijkstra(s)
}
// ...Other Johnson Code
}
Could the answer be so simple? I checked it by adding simple Golang parallelism and received exactly the expected results but in less than 6 seconds! yay!
GetDist(graph, dist, "li01_01_base", "li01_to_li02")= 22148
GetDist(graph, dist, "li01_to_li02", "li02_to_li01")= 0
GetDist(graph, dist, "li02_to_li01", "li12_02_base")= 9235
GetDist(graph, dist, "li01_01_base", "li01_02_base") 21389
GetDist(graph, dist, "li01_01_base", "br01_01_base") 128172
GetDist(graph, dist, "li01_01_base", "li12_02_base") 31383
time=2024-06-16T14:27:25.075+02:00 level=DEBUG msg="time_measure 5.880306556s | trade routes calculated"
Providing the code for it:
heap.go
package trades
import (
"container/heap"
)
// An Item is something we manage in a priority queue.
type Item struct {
value_weight int // The value of the item; arbitrary.
priority int // The priority of the item in the queue.
// The index is needed by update and is maintained by the heap.Interface methods.
index int // The index of the item in the heap.
}
// A PriorityQueue implements heap.Interface and holds Items.
type PriorityQueue []*Item
func (pq PriorityQueue) Len() int { return len(pq) }
func (pq PriorityQueue) Less(i, j int) bool {
// We want Pop to give us the highest, not lowest, priority so we use greater than here.
return pq[i].priority > pq[j].priority
}
func (pq PriorityQueue) Swap(i, j int) {
pq[i], pq[j] = pq[j], pq[i]
pq[i].index = i
pq[j].index = j
}
func (pq *PriorityQueue) Push(x any) {
n := len(*pq)
item := x.(*Item)
item.index = n
*pq = append(*pq, item)
}
func (pq *PriorityQueue) Pop() any {
old := *pq
n := len(old)
item := old[n-1]
old[n-1] = nil // avoid memory leak
item.index = -1 // for safety
*pq = old[0 : n-1]
return item
}
// update modifies the priority and value of an Item in the queue.
func (pq *PriorityQueue) update(item *Item, value int, priority int) {
item.value_weight = value
item.priority = priority
heap.Fix(pq, item.index)
}
johnson.go
package trades
import (
"container/heap"
"math"
)
// Written based on https://www.geeksforgeeks.org/implementation-of-johnsons-algorithm-for-all-pairs-shortest-paths/
type Neighbour struct {
destination int
weight int
}
func NewNeighbour(destination int, weight int) *Neighbour {
return &Neighbour{destination: destination,
weight: weight,
}
}
type Johnson struct {
vertices int
adjacencyList [][]*Neighbour
}
// On using the below constructor,
// edges must be added manually
// to the graph using addEdge()
func NewJohnson(vertices int) *Johnson {
g := &Johnson{
vertices: vertices,
}
g.adjacencyList = make([][]*Neighbour, vertices)
for i := 0; i < vertices; i++ {
g.adjacencyList[i] = make([]*Neighbour, 0)
}
return g
}
// // On using the below constructor,
// // edges will be added automatically
// // to the graph using the adjacency matrix
func NewJohnsonFromMatrix(vertices int, adjacencyMatrix [][]int) *Johnson {
g := NewJohnson(vertices)
for i := 0; i < vertices; i++ {
for j := 0; j < vertices; j++ {
if adjacencyMatrix[i][j] != 0 {
g.addEdge(i, j, adjacencyMatrix[i][j])
}
}
}
return g
}
func NewJohnsonFromGraph(graph *GameGraph) *Johnson {
vertices := len(graph.matrix)
g := NewJohnson(vertices)
index := 0
for vertex, _ := range graph.matrix {
graph.IndexByNick[vertex] = index
index++
}
for vertex_name, vertex := range graph.matrix {
for vertex_target, weight := range vertex {
i := graph.IndexByNick[vertex_name]
j := graph.IndexByNick[vertex_target]
g.addEdge(i, j, int(weight))
}
}
return g
}
func (g *Johnson) addEdge(source int, destination int, weight int) {
g.adjacencyList[source] = append(g.adjacencyList[source], NewNeighbour(destination, weight))
}
func ArraysFill[T any](array []T, value T) {
for i := 0; i < len(array); i++ {
array[i] = value
}
}
// Dijkstra which is faster than regular one with O(|V|^2)
// This is Dijkstra with heap priority queue. Compltexity O(|E|+|V|log|V|)
// According to wiki page https://en.wikipedia.org/wiki/Dijkstra's_algorithm
func (g *Johnson) dijkstra(source int) []int {
var distance []int = make([]int, g.vertices)
pq := make(PriorityQueue, 0)
item := &Item{
value_weight: 0,
priority: source,
}
pq.Push(item)
ArraysFill(distance, math.MaxInt)
distance[source] = 0
for pq.Len() > 0 {
item := heap.Pop(&pq).(*Item)
node := item.priority
dist := item.value_weight
for _, neighbour := range g.adjacencyList[node] {
if dist+neighbour.weight < distance[neighbour.destination] {
distance[neighbour.destination] = dist + neighbour.weight
pq.Push(&Item{
value_weight: distance[neighbour.destination],
priority: neighbour.destination,
})
}
}
}
return distance
}
// // Returns null if
// // negative weight cycle is detected
func (g *Johnson) bellmanford(source int) []int {
var distance []int = make([]int, g.vertices)
ArraysFill(distance, math.MaxInt)
distance[source] = 0
for i := 0; i < g.vertices-1; i++ {
for currentVertex := 0; currentVertex < g.vertices; currentVertex++ {
for _, neighbour := range g.adjacencyList[currentVertex] {
if distance[currentVertex] != math.MaxInt && distance[currentVertex]+neighbour.weight < distance[neighbour.destination] {
distance[neighbour.destination] = distance[currentVertex] + neighbour.weight
}
}
}
}
for currentVertex := 0; currentVertex < g.vertices; currentVertex++ {
for _, neighbour := range g.adjacencyList[currentVertex] {
if distance[currentVertex] != math.MaxInt && distance[currentVertex]+neighbour.weight < distance[neighbour.destination] {
return nil
}
}
}
return distance
}
func remove[T any](slice []T, s int) []T {
return append(slice[:s], slice[s+1:]...)
}
type DijkstraResult struct {
source int
dist_result []int
}
// // Returns null if negative
// // weight cycle is detected
func (g *Johnson) Johnsons() [][]int {
// Add a new vertex q to the original graph,
// connected by zero-weight edges to
// all the other vertices of the graph
g.vertices++
g.adjacencyList = append(g.adjacencyList, make([]*Neighbour, 0))
for i := 0; i < g.vertices-1; i++ {
g.adjacencyList[g.vertices-1] = append(g.adjacencyList[g.vertices-1], NewNeighbour(i, 0))
}
// Use bellman ford with the new vertex q
// as source, to find for each vertex v
// the minimum weight h(v) of a path
// from q to v.
// If this step detects a negative cycle,
// the algorithm is terminated.
var h []int = g.bellmanford(g.vertices - 1)
if h == nil {
return nil
}
// Re-weight the edges of the original graph using
// the values computed by the Bellman-Ford
// algorithm. w'(u, v) = w(u, v) + h(u) - h(v).
for u := 0; u < g.vertices; u++ {
neighbours := g.adjacencyList[u]
for _, neighbour := range neighbours {
var v int = neighbour.destination
var w int = neighbour.weight
// new weight
neighbour.weight = w + h[u] - h[v]
}
}
// Step 4: Remove edge q and apply Dijkstra
// from each node s to every other vertex
// in the re-weighted graph
g.adjacencyList = remove(g.adjacencyList, g.vertices-1)
g.vertices--
var distances [][]int = make([][]int, g.vertices)
is_sequential := false
if is_sequential {
for s := 0; s < g.vertices; s++ {
distances[s] = g.dijkstra(s)
}
} else {
dijkstra_results := make(chan *DijkstraResult)
for s := 0; s < g.vertices; s++ {
go func(s int) {
dist_result := g.dijkstra(s)
dijkstra_results <- &DijkstraResult{
source: s,
dist_result: dist_result,
}
}(s)
}
for s := 0; s < g.vertices; s++ {
result := <-dijkstra_results
distances[result.source] = result.dist_result
}
}
// Compute the distance in the original graph
// by adding h[v] - h[u] to the
// distance returned by dijkstra
for u := 0; u < g.vertices; u++ {
for v := 0; v < g.vertices; v++ {
// If no edge exist, continue
if distances[u][v] == math.MaxInt {
continue
}
distances[u][v] += (h[v] - h[u])
}
}
return distances
}
johnson_test.go
package trades
import (
"fmt"
"math"
"testing"
)
// // Driver Code
func TestJohnson(t *testing.T) {
var vertices int = 4
var matrix [][]int = [][]int{
{0, 0, -2, 0},
{4, 0, 3, 0},
{0, 0, 0, 2},
{0, -1, 0, 0},
}
// Initialization
var graph *Johnson = NewJohnsonFromMatrix(vertices, matrix)
// Function Call
var distances [][]int = graph.Johnsons()
if distances == nil {
fmt.Println("Negative weight cycle detected.")
return
}
// The code fragment below outputs
// an formatted distance matrix.
// Its first row and first
// column represent vertices
fmt.Println("Distance matrix:")
fmt.Printf(" \t")
for i := 0; i < vertices; i++ {
fmt.Printf("%3d\t", i)
}
for i := 0; i < vertices; i++ {
fmt.Println()
fmt.Printf("%3d\t", i)
for j := 0; j < vertices; j++ {
if distances[i][j] == math.MaxInt {
fmt.Printf(" X\t")
} else {
fmt.Printf("%3d\t",
distances[i][j])
}
}
}
}
func TestJsonsoner(t *testing.T) {
fmt.Println(math.MaxFloat32)
graph := NewGameGraph()
graph.SetEdge("a", "b", 5)
graph.SetEdge("a", "d", 10)
graph.SetEdge("b", "c", 3)
graph.SetEdge("c", "d", 1)
johnson := NewJohnsonFromGraph(graph)
var dist [][]int = johnson.Johnsons()
for i := 0; i < 4; i++ {
for j := 0; j < 4; j++ {
if dist[i][j] == math.MaxInt {
fmt.Printf("%7s", "INF")
} else {
fmt.Printf("%7d", dist[i][j])
}
}
fmt.Println()
}
fmt.Println("a -> c = ", GetDist(graph, dist, "a", "c"))
fmt.Println("a -> b = ", GetDist(graph, dist, "a", "b"))
fmt.Println("a -> b = ", GetDist(graph, dist, "a", "d"))
}
That was a success! The calculation was sped up significantly with a touch of a very simple Golang parallelism using go routines and channels to collect the result; it went way faster without changing answer/result values. We went from 2 minutes and 20 seconds (technically 1 minute) to the achieved 6 seconds results for 2218 vertices, and 30250 edges, which was very satisfying and 34 times faster. The same code can be found in Github folders

Found the wiki page containing three different parallel methods for all shortest paths problem solving. The parallelizing Dijkstra solution made for Johnson’s algo looks like the DijkstraAPSP described in it. There is room to try the advanced choices for Dijkstra parallelization (that will have potentially no gain), and Floyd parallelization.
Resources to find exact realizations for those different options are very scarce though. We could optimize by skipping calculations for all shortest paths originating from vertices I use only as intermediate travel points, so we can replace for them Dijkstra calculations with a filled array [Inf, Inf, Inf, 0(for source index), Inf, Inf, Inf...] instead of calculating Dijkstra itself. The given task requires me to get distances starting from intermediate traveling points too, and I was able to modify the Dijkstra algorithm slightly further by returning more efficiently edge weights during path reconstructions, so I applied this modification.
Alternatively, there is another possible optimization. The given domain of data has as dense connections only specific star systems, with all vertices interconnected, and very scarcely only by a few edges between star systems. We could have calculated rapidly all shortest paths for each system (even with floyd), and then we could have built a second graph that contains only “space bases” and jump gates/holes connecting star systems. That would have decreased the number of vertices from 2218 to less than 900 vertices and made faster potential total calculations. But this optimization was not made, because there is a simple alternative.
The given domain of data inside each star system contains spaceship flight speed boosters called Trade Lanes. They are made out of multiple rings connected in a line. Originally each ring had its own vertex connected with edges to its neighbors. I applied optimization by joining intermediate vertices in a single trade lane, and thus the number of vertices decreased from 2218 to 1218 without almost no drop in the quality of calculations.
Additionally, optimization was made by removing Johnson’s algorithm parts. Since the graph actually had no edges with negative weights… Johnson’s Algorithm was not really required. So it was stripped down to DijkstraAPSP already written inside of it.
This final optimization gave me initially 1.5 seconds total time for calculation runs between all vertices, and it improved to 0.65s time after I white-listed in addition to running single sourced Dijkstra only for the list of allowed starting points to find out the necessary shortest trading route distances between space bases in a galaxy of a space simulator, and that is a satisfying end result for 1218 vertices, having 22896 edges in a directed graph.
Since we used DijkstraAPSP, it was possible to modify the algorithm for returning reconstructed shortest exact paths. That was very desirable for the task goals, and thankfully possible. Modifications were made based on the Wiki article for Dijkstra algo
Providing the most final DijkstraAPSP algorithm, calculating all shortest paths through DijkstraSSSP in Golang, with the provided ability for path reconstructions.
graph.go
package trades
import (
"math"
"reflect"
)
type VertexName string
type GameGraph struct {
matrix map[VertexName]map[VertexName]float64
IndexByNick map[VertexName]int
NicknameByIndex map[int]VertexName
}
func NewGameGraph() *GameGraph {
return &GameGraph{
matrix: make(map[VertexName]map[VertexName]float64),
IndexByNick: map[VertexName]int{},
NicknameByIndex: make(map[int]VertexName),
}
}
func (f *GameGraph) SetEdge(keya string, keyb string, distance float64) {
vertex, vertex_exists := f.matrix[VertexName(keya)]
if !vertex_exists {
vertex = make(map[VertexName]float64)
f.matrix[VertexName(keya)] = vertex
}
if _, vert_target_exists := f.matrix[VertexName(keyb)]; !vert_target_exists {
f.matrix[VertexName(keyb)] = make(map[VertexName]float64)
}
// Insert safety if u wish to set value only once without overriding
// _, already_set := vertex[VertexName(keyb)]
// if already_set {
// return
// }
vertex[VertexName(keyb)] = distance
}
func GetDist(f *GameGraph, dist [][]int, keya string, keyb string) int {
sourse_index, source_found := f.IndexByNick[VertexName(keya)]
target_index, target_found := f.IndexByNick[VertexName(keyb)]
_ = source_found
if !source_found || !target_found {
return math.MaxInt
}
return dist[sourse_index][target_index]
}
type Path struct {
Node int
NextNode int
Dist int
}
func GetPath(graph *GameGraph, parents [][]int, dist [][]int, source_key string, target_key string) []Path {
// fmt.Println("get_path", source_key, target_key)
S := []Path{}
u, found_u := graph.IndexByNick[VertexName(target_key)] // target
if !found_u {
return []Path{}
}
_ = found_u
source := graph.IndexByNick[VertexName(source_key)]
add_node := func(u int) {
path_to_add := Path{
Node: u,
}
if len(S) > 0 {
path_to_add.NextNode = S[len(S)-1].Node
} else {
path_to_add.NextNode = NO_PARENT
}
if path_to_add.Node != NO_PARENT && path_to_add.NextNode != NO_PARENT {
path_to_add.Dist = dist[path_to_add.Node][path_to_add.NextNode]
}
S = append(S, path_to_add)
}
add_node(u)
if parents[source][u] != NO_PARENT || u == source {
for {
u = parents[source][u]
add_node(u)
if u == NO_PARENT {
break
}
}
}
ReverseSlice(S)
return S
}
// panic if s is not a slice
func ReverseSlice(s interface{}) {
size := reflect.ValueOf(s).Len()
swap := reflect.Swapper(s)
for i, j := 0, size-1; i < j; i, j = i+1, j-1 {
swap(i, j)
}
}
type DetailedPath struct {
PrevName string
NextName string
PrevNode int
NextNode int
Dist int
}
func (graph *GameGraph) GetPaths(parents [][]int, dist [][]int, source_key string, target_key string) []DetailedPath {
var detailed_paths []DetailedPath
paths := GetPath(graph, parents, dist, source_key, target_key)
for _, path := range paths {
detailed_path := DetailedPath{
PrevName: string(graph.NicknameByIndex[path.Node]),
NextName: string(graph.NicknameByIndex[path.NextNode]),
PrevNode: path.Node,
NextNode: path.NextNode,
Dist: path.Dist,
}
detailed_paths = append(detailed_paths, detailed_path)
}
return detailed_paths
}
dijkstra_apsp.go
package trades
import (
"container/heap"
"math"
)
// Written based on https://www.geeksforgeeks.org/implementation-of-johnsons-algorithm-for-all-pairs-shortest-paths/
// And then rewritten in a way that there is nothing left from Johnson almost.
// It is now DijkstraAPSP https://en.wikipedia.org/wiki/Parallel_all-pairs_shortest_path_algorithm
type DijkstraAPSP struct {
vertices int
adjacencyList [][]*Neighbour
}
const INF = math.MaxInt
// On using the below constructor,
// edges must be added manually
// to the graph using addEdge()
func NewDijkstraApsp(vertices int) *DijkstraAPSP {
g := &DijkstraAPSP{
vertices: vertices,
}
g.adjacencyList = make([][]*Neighbour, vertices)
for i := 0; i < vertices; i++ {
g.adjacencyList[i] = make([]*Neighbour, 0)
}
return g
}
// // On using the below constructor,
// // edges will be added automatically
// // to the graph using the adjacency matrix
func NewDijkstraApspFromMatrix(vertices int, adjacencyMatrix [][]int) *DijkstraAPSP {
g := NewDijkstraApsp(vertices)
for i := 0; i < vertices; i++ {
for j := 0; j < vertices; j++ {
if adjacencyMatrix[i][j] != 0 {
g.addEdge(i, j, adjacencyMatrix[i][j])
}
}
}
return g
}
type DijkstraOption func(graph *DijkstraAPSP)
func NewDijkstraApspFromGraph(graph *GameGraph, opts ...DijkstraOption) *DijkstraAPSP {
vertices := len(graph.matrix)
g := NewDijkstraApsp(vertices)
index := 0
for vertex, _ := range graph.matrix {
graph.IndexByNick[vertex] = index
graph.NicknameByIndex[index] = vertex
index++
}
for vertex_name, vertex := range graph.matrix {
for vertex_target, weight := range vertex {
i := graph.IndexByNick[vertex_name]
j := graph.IndexByNick[vertex_target]
g.addEdge(i, j, int(weight))
}
}
for _, opt := range opts {
opt(g)
}
return g
}
func (g *DijkstraAPSP) addEdge(source int, destination int, weight int) {
g.adjacencyList[source] = append(g.adjacencyList[source], NewNeighbour(destination, weight))
}
// Dijkstra which is faster than regular one with O(|V|^2)
// This is Dijkstra with heap priority queue. Compltexity O(|E|+|V|log|V|)
// According to wiki page https://en.wikipedia.org/wiki/Dijkstra's_algorithm
func (g *DijkstraAPSP) dijkstra(source int) ([]int, []int) {
var distance []int = make([]int, g.vertices)
// this page https://en.wikipedia.org/wiki/Dijkstra%27s_algorithm
// helped to modify algorithm so it would return reconstructed paths.
// Parent array to store shortest
// path tree
var parents []int = make([]int, g.vertices)
// The starting vertex does not
// have a parent
for s := 0; s < g.vertices; s++ {
parents[s] = NO_PARENT
}
pq := make(PriorityQueue, 0)
item := &Item{
value_weight: 0,
priority: source,
}
pq.Push(item)
ArraysFill(distance, INF)
distance[source] = 0
for pq.Len() > 0 {
item := heap.Pop(&pq).(*Item)
node := item.priority
dist := item.value_weight
for _, neighbour := range g.adjacencyList[node] {
if dist+neighbour.weight < distance[neighbour.destination] {
parents[neighbour.destination] = node
distance[neighbour.destination] = dist + neighbour.weight
pq.Push(&Item{
value_weight: distance[neighbour.destination],
priority: neighbour.destination,
})
}
}
}
return distance, parents
}
type DijkstraRes struct {
source int
dist_result []int
parents_result []int
}
const NO_PARENT = -1
func (g *DijkstraAPSP) DijkstraApsp() ([][]int, [][]int) {
var distances [][]int = make([][]int, g.vertices)
var parents [][]int = make([][]int, g.vertices)
// it is nice to keep sanity by keeping optional switch removing parallelism
is_sequential := false
if is_sequential {
for s := 0; s < g.vertices; s++ {
dist_result, parents_result := g.dijkstra(s)
distances[s] = dist_result
parents[s] = parents_result
}
} else {
dijkstra_results := make(chan *DijkstraRes)
awaited := 0
for s := 0; s < g.vertices; s++ {
awaited += 1
go func(s int) {
dist_result, parents_result := g.dijkstra(s)
dijkstra_results <- &DijkstraRes{
source: s,
dist_result: dist_result,
parents_result: parents_result,
}
}(s)
}
for s := 0; s < awaited; s++ {
result := <-dijkstra_results
distances[result.source] = result.dist_result
parents[result.source] = result.parents_result
}
}
return distances, parents
}
dijkstra_apsp_test.go
package trades
import (
"fmt"
"math"
"testing"
)
// // Driver Code
func TestDijkstraAPSP(t *testing.T) {
var vertices int = 4
var matrix [][]int = [][]int{
{0, 0, 2, 0},
{4, 0, 3, 0},
{0, 0, 0, 2},
{0, 1, 0, 0},
}
// Initialization
var graph *DijkstraAPSP = NewDijkstraApspFromMatrix(vertices, matrix)
// Function Call
distances, parents := graph.DijkstraApsp()
_ = parents
// The code fragment below outputs
// an formatted distance matrix.
// Its first row and first
// column represent vertices
fmt.Println("Distance matrix:")
fmt.Printf(" \t")
for i := 0; i < vertices; i++ {
fmt.Printf("%3d\t", i)
}
for i := 0; i < vertices; i++ {
fmt.Println()
fmt.Printf("%3d\t", i)
for j := 0; j < vertices; j++ {
if distances[i][j] == math.MaxInt {
fmt.Printf(" X\t")
} else {
fmt.Printf("%3d\t",
distances[i][j])
}
}
}
}
func TestDijkstraAPSPWithGraph(t *testing.T) {
graph := NewGameGraph()
graph.SetEdge("a", "b", 5)
graph.SetEdge("a", "d", 10)
graph.SetEdge("b", "c", 3)
graph.SetEdge("c", "d", 1)
johnson := NewDijkstraApspFromGraph(graph)
dist, parents := johnson.DijkstraApsp()
fmt.Println("solved matrix")
for i := 0; i < 4; i++ {
for j := 0; j < 4; j++ {
if dist[i][j] == math.MaxInt {
fmt.Printf("%7s", "INF")
} else {
fmt.Printf("%7d", dist[i][j])
}
}
fmt.Println()
}
fmt.Println("get dists and paths")
fmt.Println("a -> c = ", GetDist(graph, dist, "a", "c"), "path=", graph.GetPaths(parents, dist, "a", "c"))
fmt.Println("a -> b = ", GetDist(graph, dist, "a", "b"), "path=", GetPath(graph, parents, dist, "a", "b"))
fmt.Println("a -> d = ", GetDist(graph, dist, "a", "d"), "path=", GetPath(graph, parents, dist, "a", "d"))
fmt.Println("detailed path reconstruction, useful for debug")
paths := graph.GetPaths(parents, dist, "a", "c")
for index, path := range paths {
if path.Dist == 0 && (index != 0 || index != len(paths)-1) {
continue
}
fmt.Println(
fmt.Sprintf("prev= %20s", path.PrevName),
fmt.Sprintf("next= %20s", path.NextName),
fmt.Sprintf("prev_node= %5d", path.PrevNode),
fmt.Sprintf("next_node= %5d", path.NextNode),
fmt.Sprintf("dist= %5d", path.Dist),
)
}
}
TestDijkstraAPSPWithGraph output:
solved matrix
0 5 9 8
INF 0 4 3
INF INF 0 INF
INF INF 1 0
get dists and paths
a -> c = 8 path= [{ a -1 0 0} {a b 0 1 5} {b c 1 3 3} {c 3 -1 0}]
a -> b = 5 path= [{-1 0 0} {0 1 5} {1 -1 0}]
a -> d = 9 path= [{-1 0 0} {0 1 5} {1 3 3} {3 2 1} {2 -1 0}]
detailed path reconstruction, useful for debug
prev= a next= b prev_node= 0 next_node= 1 dist= 5
prev= b next= c prev_node= 1 next_node= 3 dist= 3
PASS
Attachments:
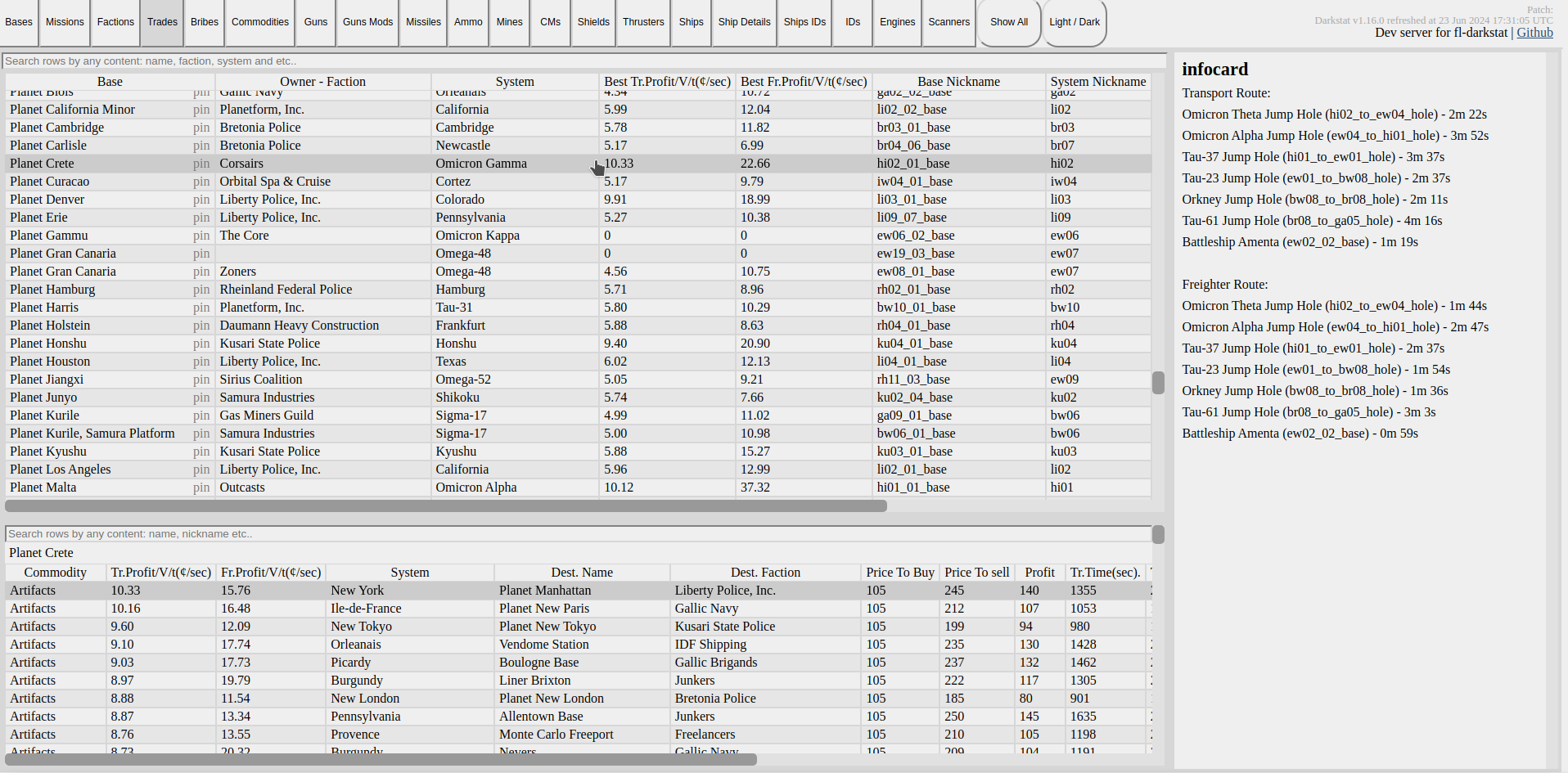
All examples have unit tests on how to use them ^_^. The links above may contain a version of the article and code examples more up-to-date or with other fixes. The research results were applied to darkstat tool for trading route calculations between space bases in the Freelancer Discovery modding community.
DarkStat trading routes tab: